17.) Define the terms incenter, circumcenter, orthocenter, and centroid. Now draw a sketch of each of these terms.

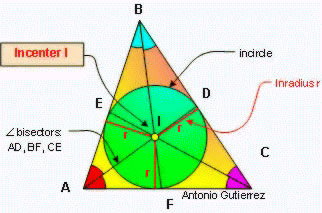
This is the incenter of the triangle. An incenter is the point at which the angle bisector of a triangle intersect. It is also described as the center of the circle that can be inscribed in the triangle.

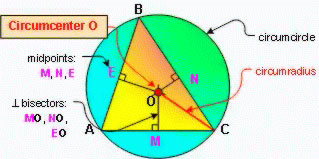
This is the circumcenter of the triangle. A circumcenter is the point at which the three perpendicular bisectors of each side of the triangle intersect. It is also described as the center of the circle that can be circumscribed about the triangle.

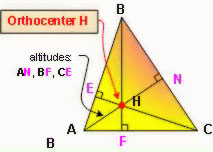
This is the orthocenter of the triangle. An orthocenter is the point at which the altitudes of a triangle intersect.

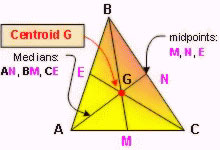
This is the centroid of the triangle. A centroid is the point at which the medians of the triangle intersect. It is also considered the center of gravity of the triangle.

This information was found at http://www.geom.uiuc.edu/~demo5337/Group2/indef.html

The pictures were found at http://agutie.homestead.com/files/Trianglecenter_B.htm